Senin, 27 Februari 2012

Matriks

17.37  Nerazurri  No comments

Matriks adalah kumpulan bilangan berbentuk persegi panjang yang disusun menurut baris dan kolom. Bilangan-bilangan yang terdapat di suatu matriks disebut dengan elemen atau anggota matriks. Dengan representasi matriks, perhitungan dapat dilakukan dengan lebih terstruktur. Pemanfaatannya misalnya dalam menjelaskan persamaan linier, transformasi koordinat, dan lainnya. Matriks seperti halnya variabel biasa dapat dimanipulasi, seperti dikalikan, dijumlah, dikurangkan dan didekomposisikan.
A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{bmatrix} \!

Penjumlahan dan pengurangan matriks

Penjumlahan dan pengurangan matriks hanya dapat dilakukan apabila kedua matriks memiliki ukuran atau tipe yang sama. Elemen-elemen yang dijumlahkan atau dikurangi adalah elemen yang posisi atau letaknya sama.
a_{ij} \pm b_{ij} = c_{ij}\!
atau dalam representasi dekoratfinya
\begin{bmatrix} {3} & {4} \\ {6} & {5} \\ \end{bmatrix} \!
\begin{bmatrix} (a_{11} \pm b_{11}) & (a_{12} \pm b_{12}) & (a_{13} \pm b_{13}) \\ (a_{21} \pm b_{21}) & (a_{22} \pm b_{22}) & (a_{23} \pm b_{23}) \\ \end{bmatrix} = \begin{bmatrix} c_{11} & c_{12} & c_{13} \\ c_{21} & c_{22} & c_{23} \\ \end{bmatrix} \!

Perkalian Skalar

Matriks dapat dikalikan dengan sebuah skalar.
\lambda\cdot A := (\lambda\cdot a_{ij})_{i=1, \ldots , m; \ j=1, \ldots , n}
Contoh perhitungan :
5 \cdot \begin{pmatrix} 1 & -3 & 2 \\ 1 & 2 & 7 \end{pmatrix} = \begin{pmatrix} 5 \cdot 1 & 5 \cdot (-3) & 5 \cdot 2 \\ 5 \cdot 1 & 5 \cdot 2 & 5 \cdot 7 \end{pmatrix} = \begin{pmatrix} 5 & -15 & 10 \\ 5 & 10 & 35 \end{pmatrix}

Perkalian matriks

Matriks dapat dikalikan, dengan cara tiap baris dikalikan dengan tiap kolom, lalu dijumlahkan pada baris yang sama.
c_{ij}=\sum_{k=1}^m a_{ik}\cdot b_{kj}
Contoh perhitungan :

\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{pmatrix} \cdot \begin{pmatrix} 6 & -1 \\ 3 & 2 \\ 0 & -3 \end{pmatrix} = \begin{pmatrix} 1 \cdot 6 + 2 \cdot 3 + 3 \cdot 0 & 1 \cdot (-1) + 2 \cdot 2 + 3 \cdot (-3) \\ 4 \cdot 6 + 5 \cdot 3 + 6 \cdot 0 & 4 \cdot (-1) + 5 \cdot 2 + 6 \cdot (-3) \\ \end{pmatrix} = \begin{pmatrix} 12 & -6 \\ 39 & -12 \end{pmatrix}

Invers Dan Determinan Matriks


Matriks 3x3
Matriks 3x3
Mencoba memenuhi permintaan dari sobat Bryan untuk posting tentang invers dan determinan matriks, maka pada postingan kali ini akan mencoba membahas sedikit materi yang berkaitan dengan invers dan determinan matriks.
Matriks merupakan susunan bilangan-bilangan berbentuk persegi atau persegi panjang yang diatur menurut baris dan kolom tertentu. Matriks dinotasikan dengan huruf kapital. Jika m adalah banyaknya baris dari matriks A, dan n adalah banyaknya kolom dari matriks A, maka matriks A mempunyai ordo m \times n, atau ditulis A_{m\times n}.
A_{m \times n} = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \cdots &\vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}

1. Invers Matriks

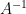Jika A dan B adalah matriks persegi, dan berlaku A \cdot B = B \cdot A = I maka dikatakan matriks A dan B saling invers. B disebut invers dari A, atau ditulis A^{-1}. Matriks yang mempunyai invers disebut invertible atau matriks non singular, sedangkan matriks yang tidak mempunyai invers disebut matriks singular.
Untuk mencari invers matriks persegi berordo 2×2, coba perhatikan berikut ini.
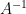Jika A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} dengan ad - bc \neq 0, maka invers dari matriks A (ditulis A^{-1}) adalah sebagai berikut:
A^{-1} = \frac {1}{ad - bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}
Jika ad - bc = 0 maka matriks tersebut tidak mempunyai invers, atau disebut matriks singular.
Sifat-sifat matriks persegi yang mempunyai invers:
  • (A \cdot B)^{-1} = B^{-1} \cdot A^{-1}
  • (B \cdot A)^{-1} = A^{-1} \cdot B^{-1}
  • (A^{-1})^t =(A^{t})^{-1}
Contoh: Tentukan invers dari matriks berikut!
\begin {array} {lcl} A & = & \begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix} \\ A^{-1} & = & \frac {1}{2 \times 3 - 1 \times 5} \begin{bmatrix} 3 & -5 \\ -1 & 2 \end{bmatrix} \\ & = & \frac {1}{6-5} \begin{bmatrix} 3 & -5 \\ -1 & 2 \end{bmatrix} \\ & = & \frac {1}{1} \begin{bmatrix} 3 & -5 \\ -1 & 2 \end{bmatrix} \\ A^{-1} & = & \begin{bmatrix} 3 & -5 \\ -1 & 2 \end{bmatrix}\end{array}

2. Determinan Matriks

Syarat suatu matriks dapat dicari determinannya adalah matriks tersebut harus merupakan matriks persegi. Jika A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}, maka rumus untuk mencari determinan matriks berordo 2×2:
det A = \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad - bc
Sedangkan untuk mencari determinan matriks berordo 3×3 menggunakan aturan Sarrus.
A_{3 \times 3} = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{2n}\\ a_{31} & a_{32} & a_{33} \end{bmatrix}
\begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{2n}\\ a_{31} & a_{32} & a_{33} \end{vmatrix} \begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{matrix}
\begin{array} {lcl} \begin{vmatrix} A \end{vmatrix} = && a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} \\ & - & a_{13}a_{22}a_{31} - a_{11}a_{23}a_{32} - a_{12}a_{21}a_{33} \end{array}
Contoh: Tentukan determinan dari matriks berikut!
A = \begin{bmatrix} 3 & 1 \\ 5 & 2 \end{bmatrix}
\begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 3 & 1 \\ 5 & 2 \end{vmatrix} = 3 \times 2 - 1 \times 5 = 6 - 5 = 1
B = \begin{bmatrix} 1 & 2 & 3 \\ 1 & 3 & 4\\ 1 & 4 & 3 \end{bmatrix}
\begin{vmatrix} B \end{vmatrix} = \begin{vmatrix}1 & 2 & 3 \\ 1 & 3 & 4\\ 1 & 4 & 3 \end{vmatrix} \begin{matrix} 1 & 2\\ 1 & 3 \\ 1 & 4 \end{matrix}
\begin{array} {lcl} \begin{vmatrix} B \end{vmatrix} & = & 1.3.3 + 2.4.1 + 3.1.4 - 1.3.3 - 4.4.1 - 3.1.2 \\ & = & 9 + 8 + 12 - 9 - 16 - 6 \\ & = & -2 \end{array}

Posted in:

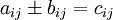
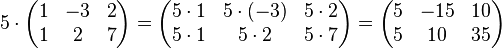
0 komentar:

Posting Komentar