Definisi
Jika terdapat himpunan A dan himpunan B (A bisa sama dengan B), maka relasi R dari A ke B adalah subhimpunan dari A×B.
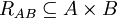
Relasi dan fungsi proposisi
Sebuah relasi dapat dikaitkan dengan sebuah fungsi proposisi atau kalimat terbuka yang himpunan penyelesaiannya tidak lain adalah relasi tersebut.
Sebagai contoh, pandang himpunan B = { apel, jeruk, mangga, pisang } dengan himpunan W = { hijau, kuning, orange}. Suatu relasi R dari Ake B didefinisikan sebagai R = {(apel, hijau), (jeruk, orange), (mangga, hijau), (pisang, kuning)}. Terdapat fungsi proposisi w(x, y) = "xberwarna y", yang himpunan penyelesaiannya adalah {(apel, hijau), (jeruk, orange), (mangga, hijau), (pisang, kuning)}, yang tidak lain adalah relasi R.
Relasi A×A
Sebuah relasi A×A, yaitu relasi dari himpunan A kepada A sendiri, dapat memiliki sifat-sifat berikut:
- Refleksif
- Irefleksif
- Simetrik
- Anti-simetrik
- Transitif
Kita menyebut relasi R dari A kepada A sebagai relasi R dalam A.
Relasi Refleksif
Sebuah relasi R dalam A disebut memiliki sifat refleksif, jika setiap elemen A berhubungan dengan dirinya sendiri.

atau

Contoh relasi yang memiliki sifat seperti ini adalah relasi “x selalu bersama y.”, dengan x dan y adalah anggota himpunan seluruh manusia. Jelas sekali bahwa setiap orang pasti selalu bersama dengan dirinya sendiri.
Relasi Irefleksif
Relasi R dalam A disebut memiliki sifat irefleksif, jika setiap elemen A tidak berhubungan dengan dirinya sendiri.

atau

Contoh relasi irefleksif adalah relasi “x mampu mencukur rambut y dengan rapi sempurna.”, dengan x dan y adalah setiap pemotong rambut. Diandaikan bahwa setiap orang hanya dapat mencukur rambut orang lain dengan rapi sempurna, maka relasi ini adalah irefleksif, karena tidak ada seorang tukang cukur a yang mampu mencukur rambutnya sendiri.
Contoh lain dalam himpunan bilangan bulat adalah, relasi < dan > adalah irefleksif.
Relasi Simetrik
Relasi R dalam A disebut memiliki sifat simetrik, jika setiap pasangan anggota A berhubungan satu sama lain. Dengan kata lain, jika aterhubung dengan b, maka b juga terhubung dengan a. Jadi terdapat hubungan timbal balik.

atau

Sebuah relasi “x + y genap” adalah relasi simetrik, karena untuk sembarang x dan y yang kita pilih, jika memenuhi relasi tersebut, maka dengan menukarkan nilai y dan x, relasi tersebut tetap dipenuhi. Misalnya untuk pasangan (5, 3) relasi tersebut dipenuhi, dan untuk (3, 5) juga.
Relasi Anti-simetrik
Jika setiap a dan b yang terhubung hanya terhubung salah satunya saja (dengan asumsi a dan b berlainan), maka relasi macam ini disebut relasi anti-simetrik.

atau

Dalam kebanyakan literatur biasanya ditulis sebagai kontraposisinya seperti di bawah ini. Keuntungan bentuk ini adalah tidak mengandung negasi, dan hanya mengandung satu implikasi.

atau

Relasi  bersifat anti-simetrik, karena
bersifat anti-simetrik, karena  mengakibatkan
mengakibatkan  . Demikian juga jika ada p dan q yang terhadap mereka berlaku
. Demikian juga jika ada p dan q yang terhadap mereka berlaku 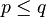 dan
dan 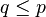 berarti p = q.
berarti p = q.
Relasi Transitif
Sebuah relasi disebut transitif jika memiliki sifat, jika a berhubungan dengan b, dan b berhubungan dengan c, maka a berhubungan dengan csecara langsung.

atau

Sebagai contoh, relasi dua transitif. Misalnya untuk 5, 6, dan 7, berlaku 5 < 6, 6 < 7, dan 5 < 7.
Relasi khusus
Relasi Ekivalen
Sebuah relasi disebut sebagai relasi ekivalen jika relasi tersebut bersifat:
- Refleksif
- Simetrik, dan
- Transitif
Relasi ekuivalen memiliki hubungan erat dengan partisi, yang merupakan alasan mengapa partisi dari sebuah himpunan disebut kelas ekivalen atau kelas kesetaraan.
Orde Parsial
Orde parsial adalah relasi yang bersifat:
- Refleksif
- Anti-simetrik, dan
- Transitif
 bersifat anti-simetrik, karena
bersifat anti-simetrik, karena  mengakibatkan
mengakibatkan  . Demikian juga jika ada p dan q yang terhadap mereka berlaku
. Demikian juga jika ada p dan q yang terhadap mereka berlaku 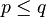 dan
dan 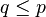 berarti p = q.
berarti p = q.
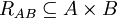













0 komentar:
Posting Komentar